Today we will talk about neural networks. Let's say we want to create a robot that correctly determines which piece appears on the screen in the game Tetris. I specifically looked up the names of these pieces on the Internet, they have speaking names:
So, we have the shapes I, L, O, S, T, and when, for example, the shape L appears on the screen, the robot must correctly say that it is the shape L that has appeared. So what is the problem? The problem is that our shape can rotate and be positioned in different parts of the screen. So, in both of the following cases, the robot must give us L:
Using combinatorics and group theory (which you can study with Russian Math Tutors), you can calculate that even on a 5×5 screen you can depict the shape L in 3×4×8 = 96 ways. We are too lazy to explain to the computer (or robot) for each of these cases that we are talking about the same shape. We want the computer to learn to recognize images on its own. This is what we call machine learning.
Let's move on to consider how a computer learns to recognize shapes using neural networks. A neural network consists of layers of neurons connected to each other. The first layer is called the input layer, and the last layer is called the output layer. In addition, there are intermediate (or hidden) layers of neurons, the number of which varies. The network below has just one intermediate layer:
The outer layer of the depicted network contains 4 neurons, the intermediate layer contains 5 neurons, and the output layer contains only one neuron. The number of neurons in layers depends on what problem we are solving. Namely, the number of neurons in the input layer corresponds to the amount of information that we submit to the input. On the other hand, the number of neurons in the output layer corresponds to the amount of information that the computer must return. To explain this, let's look at the left of the two L shapes above. We can split the entire image into five stripes, and then connect them into one long strip of length 25:
That is, we are able to encode one of the possible images of the shape L with a binary string of length 25: 0010000100011000000000000. This tells us that the input layer of our neural network must contain 25 neurons. In this case, each neuron of the input layer can get two values, 1 when the corresponding pixel of our image is colored and 0 when the pixel is not colored.
What happens to the output layer? Since the output should return an answer to us, which shape was received at the input, it is enough to use one neuron, which can get five values: I, L, O, S, T or 1, 2, 3, 4, 5. For convenience, we will not use intermediate layers, so our neural network that guesses the names of Tetris pieces on a 5x5 screen will have the following form:
It’s not for nothing that we named the neurons of the input layer x1, ..., x25, and the single neuron of the output layer y. From a mathematical point of view, our neural network is a function f(x1, ..., x25). Try to guess the value of:
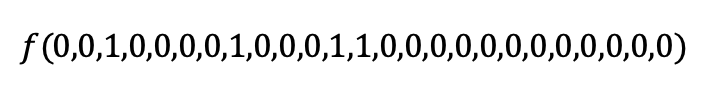
Note that the indicated variable values correspond to the line 0010000100011000000000000 written above, which corresponds to shape L, that is, the shape with number 2 in the list I, L, O, S, T. From here we know that:
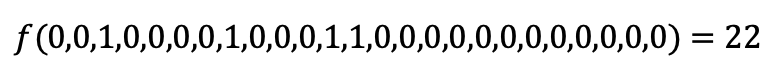
Similarly, we can verify that:

| Private Lessons | | | Group Lessons |
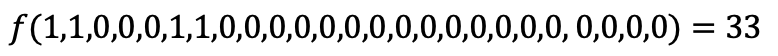
Now imagine that our function is described by the equation f(x1, ..., x25) = a1x1, ..., a25x25, with unknown coefficients a1, ..., a25 (of course in practice, we choose much more complicated equations).
The essence of machine learning, in this case, comes down to selecting the coefficients a1, ..., a25, through some known (test) values of our function (for example, those above) so that whenever we are given a shape (i.e., the corresponding variable values), the result of calculating this function equals the number of the shape. Thus, if we put a1 = ... = a25 = 1, then we get
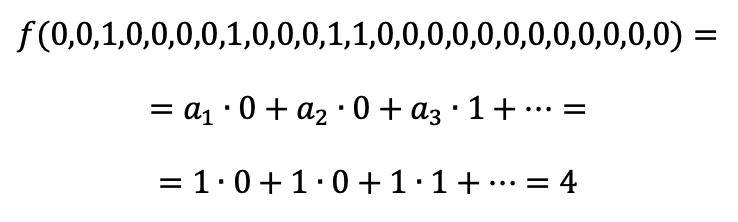
But we know that:
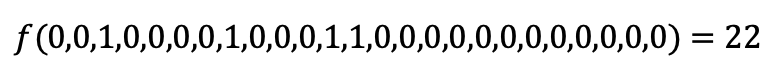
So, making all coefficients equal to 1 was not the best idea. By using appropriate algorithms (such as backpropagation), we can get better coefficients and ensure that our function returns the correct names for the Tetris pieces. Similarly, you can teach the function to recognize any photos (animals, people, cars, traffic lights, etc.) or voices.
(A bit technical) addition. Above, we’ve mentioned the "backpropagation" algorithm. This is a really powerful tool to determine the coefficients of our equation (or weights of the links between consecutive layers of neurons). In general, this equation is non-linear. That is, the predictive function f depends on several variables in a non-trivial way. What we want to do is to minimize the function f-g, where function g returns the exact names of our shapes. To minimize f-g, we may apply the gradient descent method based on finding the partial derivatives of f-g (which are studied in multi-variable calculus). The latter task is too complicated (since f-g inherits non-linearity) and this is where we apply the backpropagation by moving backward through the layers and finding the derivatives numerically.

| Private Lessons | | | Group Lessons |